Singular Value Decomposition (SVD): From Photo Puzzles to Recommendation Systems
Have you ever wondered how Netflix knows which movies you’ll love or how Spotify curates playlists that match your taste? Behind the scenes, there’s a powerful mathematical tool called Singular Value Decomposition (SVD) at work. In this blog post, we’ll unravel SVD in a simple, step-by-step manner, making it accessible to learners at all stages. We’ll start with a relatable analogy and gradually delve into how SVD powers recommendation systems.
The Photo Puzzle Analogy
Imagine you’re working on a photo puzzle. You have a beautiful image that’s been cut into many tiny pieces. The puzzle is so complex that assembling it seems overwhelming. Now, what if someone told you, “You don’t need all these pieces. Just use the most important ones, and you’ll still see the complete picture, even if some small details are missing.”
That’s essentially what SVD does in mathematics. It takes a complex matrix (like your photo), breaks it down into simpler parts, and identifies which parts are the most significant. By focusing on these key components, you can reconstruct the main idea without getting bogged down by intricate details.
Step 1: The Original Photo as a Matrix $ A $
Consider a digital photo composed of pixels. Each pixel has a color value, and collectively, these values form a matrix $ A $. For a 1000x1000 pixel image, $ A $ would be a matrix with 1,000,000 entries!
Goal of SVD: Break down this large matrix $ A $ into three smaller, more manageable matrices that capture the essential information of the original image.
Step 2: Decomposing $ A $ into Three Matrices
SVD decomposes the matrix $ A $ into three distinct components:
$$ A = U \Sigma V^T $$
- $ U $: Represents the patterns in the rows of $ A $.
- $ \Sigma $: Contains the singular values, indicating the importance of each pattern.
- $ V^T $: Represents the patterns in the columns of $ A $.
Step 3: Understanding Each Component
Matrix $ U $ — Directions for Arranging the Puzzle Pieces
- Role: Think of $ U $ as providing instructions on how to arrange the rows of your photo.
- Mathematically:
- $ U $ is an orthogonal matrix of size $ m \times m $ (e.g., 1000x1000).
- Its columns are called left singular vectors.
- These vectors capture the main patterns or features in the data.
Matrix $ \Sigma $ — The Importance of Each Piece
- Role: $ \Sigma $ tells you how important each piece is to the overall image.
- Mathematically:
- $ \Sigma $ is a diagonal matrix of size $ m \times n $ (e.g., 1000x1000).
- The diagonal entries are the singular values, sorted from largest to smallest.
- Larger singular values correspond to more significant features.
Matrix $ V^T $ — How to Combine the Pieces
- Role: $ V^T $ provides instructions on how to arrange the columns of your photo.
- Mathematically:
- $ V^T $ is an orthogonal matrix of size $ n \times n $ (e.g., 1000x1000).
- Its rows are called right singular vectors.
- These vectors capture the relationships between the columns of $ A $.
Step 4: Rebuilding the Photo with Fewer Pieces
Here’s the exciting part: You can reconstruct an approximation of the original matrix $ A $ using only the most significant singular values and their corresponding vectors.
Keeping Only the Top $ k $ Singular Values
$$ A_k = U_k \Sigma_k V_k^T $$
- $ A_k $: The approximate reconstruction of $ A $.
- $ U_k $: The first $ k $ columns of $ U $.
- $ \Sigma_k $: A diagonal matrix with the top $ k $ singular values.
- $ V_k^T $: The first $ k $ rows of $ V^T $.
By selecting a smaller $ k $, you reduce the dimensionality of the data, effectively compressing the image while retaining the most critical information.
Visual Example: Compressing an Image with SVD
Let’s say you have an image represented by a matrix $ A $. By applying SVD and keeping only the top singular values, you can:
- Reduce Storage: Store fewer numbers than the original matrix requires.
- Maintain Quality: Preserve the main features of the image.
Illustration:
- Original Image: Requires 1,000,000 numbers (for a 1000x1000 matrix).
- Compressed with Top 100 Singular Values:
- $ U_k $: 1000x100
- $ \Sigma_k $: 100x100
- $ V_k^T $: 100x1000
- Total Numbers Stored: $ (1000 \times 100) + (100 \times 100) + (100 \times 1000) = 210,000 $
You’ve reduced storage by nearly 80%!
Applications Beyond Images
While we’ve used a photo as an analogy, SVD is widely used in:
- Data Compression: Reducing the size of data while preserving essential information.
- Noise Reduction: Eliminating insignificant components that may be considered noise.
- Latent Semantic Analysis: Understanding relationships in textual data.
- Recommendation Systems: Predicting user preferences, which we’ll explore next.
SVD in Recommendation Systems
Recommendation systems aim to predict user preferences based on past interactions. SVD helps in:
- Identifying Patterns: Uncovering latent factors that influence user-item interactions.
- Dimensionality Reduction: Simplifying large user-item matrices to focus on significant patterns.
- Predicting Missing Values: Estimating how a user might rate an item they haven’t interacted with yet.
Step 1: The User-Item Matrix $ A $
Consider a matrix where:
- Rows: Represent users.
- Columns: Represent items (movies, products, etc.).
- Entries: Represent interactions (ratings, purchases).
Example:
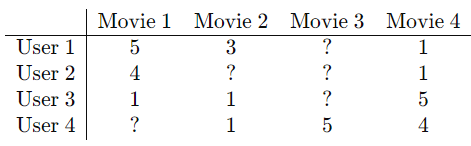
Note: The question marks represent missing values—we want to predict these.
Step 2: Applying SVD to the User-Item Matrix
We decompose $ A $ into $ U $, $ \Sigma $, and $ V^T $:
$$ A = U \Sigma V^T $$
- $ U $: Captures user preferences.
- $ \Sigma $: Highlights significant patterns.
- $ V^T $: Captures item characteristics.
Step 3: Truncated SVD for Dimensionality Reduction
To manage large datasets, we use truncated SVD, keeping only the top $ k $ singular values:
$$ A_k = U_k \Sigma_k V_k^T $$
- Reduces Noise: Focuses on significant interactions.
- Computational Efficiency: Less data to process.
Example with $ k = 2 $:
- We keep only the top 2 singular values and corresponding vectors.
Step 4: Reconstructing and Predicting Missing Values
By multiplying the truncated matrices, we get an approximate matrix $ \hat{A} $:
$$ \hat{A} = U_k \Sigma_k V_k^T $$
Reconstructed Matrix:
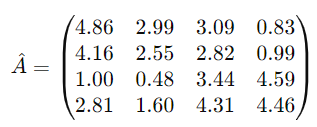
Predictions:
- User 1, Movie 3: Predicted rating is 3.09.
- User 2, Movie 2: Predicted rating is 2.55.
- User 2, Movie 3: Predicted rating is 2.82.
- User 4, Movie 1: Predicted rating is 2.81.
Understanding the Predictions
- Higher Values: Suggest the user is likely to enjoy the item.
- Lower Values: Suggest the user may not prefer the item.
- Application: The system can recommend movies with higher predicted ratings to users.
Advantages of Using SVD in Recommendation Systems
- Personalization: Tailors recommendations to individual user preferences.
- Scalability: Efficient with large datasets.
- Discovering Latent Factors: Unveils hidden patterns (e.g., genres, themes).
Challenges and Considerations
- Sparsity: User-item matrices are often sparse; SVD helps but may require additional techniques.
- Cold Start Problem: New users or items with no interactions can’t be accurately modeled initially.
- Computational Resources: Large matrices require significant computational power for decomposition.
Conclusion
Singular Value Decomposition is a versatile tool that simplifies complex data into its most essential components. Whether compressing images or powering recommendation systems, SVD helps us make sense of vast amounts of information by focusing on what’s truly important.
Further Reading:
- Matrix Decompositions: Explore other decompositions like QR and Eigenvalue decomposition.
- Advanced Recommendation Systems: Dive into collaborative filtering, content-based filtering, and hybrid models.
- Machine Learning Applications: See how SVD integrates with algorithms like Principal Component Analysis (PCA).
References:
- Strang, G. (2016). Introduction to Linear Algebra. Wellesley-Cambridge Press.
- Koren, Y., Bell, R., & Volinsky, C. (2009). Matrix Factorization Techniques for Recommender Systems. Computer, 42(8), 30-37.